Static Program Analysis
静态程序分析(Static program analysis)是指在不运行程序的条件下,进行程序分析的方法。
值得一提的是,index 被广泛的用于程序分析。
Control Flow Analysis
Data Flow Analysis
Taint Analysis可以认为是Data Flow Analysis的一种。它只关心污点数据的传播。
Pointer Analysis
Pattern Matching
根据定义,写一个正则表达式去源代码匹配有问题的语句,也算是静态分析。不过Pattern Matching不一定要在源代码上做,可以在源代码、AST、中间代码、Binary等任意地方完成。
Pattern Matching 显然是一种非常简单的方法,同时局限性也很大,他完全不考虑程序的控制流和数据流。可以结合其他静态分析的方法一起使用。
Abstract Interpretation
Abstract interpretation(抽象解释) is a technique to approximate the execution of a given computer program upon an abstract domain without concrete inputs. (例如,输入是一个int,结合具体分析任务,我们可以将它的值限制在{+, -, 0}的domain,或者是{constant, bottom} domain)
抽象解释技术的主要思想是:
- 抽象化(Abstraction): 将具体的程序状态(如变量值、控制流等)映射到一个抽象的有限域上。这个抽象域比实际的具体域要小,更易于分析和操作。
- 解释(Interpretation): 在抽象域上执行语义规则,模拟程序在这个抽象域上执行时的行为,从而推导程序在这个抽象域上的语义性质。
- 收敛(Convergence): 通过迭代方式在抽象域上执行语义规则,直到达到不动点(fixpoint),即不再发生状态变化。在这个不动点上,获得程序在该抽象域上的最终语义性质。
抽象解释的优势在于,它可以在不执行程序的情况下,对程序进行静态分析和验证,从而发现潜在的错误或未定义行为。通过选择不同粒度的抽象域,可以在精度和效率之间权衡。
具体的解释,我发现了一个非常好的文章:https://wiki.mozilla.org/Abstract_Interpretation 他里面还提供了常量传播的例子。看完它之后 #TODO ,我们再回顾上面的三个主要思想:
- Abstraction (Lattice)
- ⊤, called "top" (remember the T for top), the set of all integer values
- 1, 2, ..., the singleton sets of integer values
- ⊥, called "bottom", the empty set
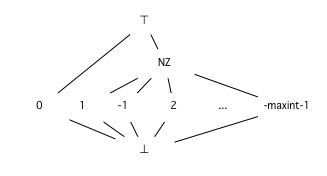
- Merging.: least upper bound (lub). e.g. \(\(1\ lub\ -1 = NZ\)\)
- Interpretation: 将原本程序语句的语义映射为格的运算。 e.g.
x:= a + 1的运算结果就是const+1 if a=const else NZ if a=NZ else T - Convergence: 不断重复这个过程,直到达到不动点。由于运算都是单调的,一定会收敛。
在南京大学的软件分析课上,李樾老师讲的分析方法就是 latice abstract interpretation. 他使用抽象解释技术,讲了数据流分析。
Symbolic Execution
符号执行的关键思想就是,把输入变为符号值,那么程序计算的输出值就是一个符号输入值的函数。在遇到程序分支指令时,程序的执行也相应地搜索每个分支,分支条件被加入到符号执行保存的程序状态的\(\pi\)中,\(\pi\)表示当前路径的约束条件。在收集了路径约束条件之后,使用约束求解器来验证约束的可解性,以确定该路径是否可达。若该路径约束可解,则说明该路径是可达的;反之,则说明该路径不可达,结束对该路径的分析。
动态符号执行
选择性符号执行
混合执行(concolic execution)
由于需要使用约束求解,而且对循环不友好,所以符号执行方法比较难以大规模应用。 经典的符号执行工具如KLEE,已经被加入LLVM的官方项目列表中。
约束求解, SAT & SMT
SAT Problem: Given a well-formed formula α in propositional logic, decide whether there exists a satisfying solution for α.
例如,\(\alpha(x,y) = x \wedge y\) SAT判定存在解x=y=1。这个问题是 NP Complete的。SMT在SAT的基础上增加了一些[一阶理论]的内容。知乎上有这样一个回答:
SMT就是SAT(布尔表达式可满足性理论)在布尔表达式的基础上拓展到其他理论,比如加上实数理论,问你 x^2+y^2=-1 是否可满足。
Z3是一个由微软开发的可满足性模理论(Satisfiability Modulo Theories,SMT)的约束求解器。yices2也是约束求解器。SMT-LIB 格式是多个 SMT 求解器使用的社区标准。它使用类似 LISP 的语法,使工具可以轻松地序列化和反序列化模型。
Formal Verification
形式化验证的3个主要问题:
- Specification:程序应该满足什么性质
- Modeling:如何表示一个程序
- Verification:如何检查程序是否满足相关性质
- 交互式验证:Coq
- 自动化验证:Seahorn,CPAChecker
- Auto-active验证:Why3,Viper,Dafny
程序验证的核心是霍尔逻辑。霍尔逻辑的核心概念是霍尔三元组,一般记为以下形式:
其中,\(P\)和\(Q\)是一阶逻辑公式,分别表示前置条件(Pre-Condition)和后置条件(Post-Condition)。 \(c\)表示一段程序源代码。 霍尔三元组的含义是,假定前置条件\(P\)是有效的,那么在执行完程序\(c\)后,后置条件\(Q\)将会是有效的。
如何处理循环,我们需要找循环不变式(Loop Invariant)。自动推导循环不变式是自动程序验证的核心任务。约束求解推导循环不变式。
模型检测(Model Checking)是一种经典的形式化分析方法。 它通过构造软件系统的抽象模型,来检测其是否满足要求的性质。 模型检测方法的缺点是系统模型的建立需要领域专家的参与。 寻找恰当的抽象层次,从而足以证明系统的特定属性,是模型检测的一大难点。 过分的抽象将导致属性无法证明;而不足的抽象又将导致太多属性无关的冗余细节,从而引发状态爆炸,无法在合理的时间内得到结果。
AI Based
现在论文里会用AI对程序进行分析。不做评价。
Reference
- https://wiki.mozilla.org/Abstract_Interpretation
- 非常好的形式化验证入门资料:https://www.zhihu.com/column/c_1311359270597419008
- hand book of model checking