Compiler
编译的大致的流程如下。下图忽略了代码优化的部分,代码的优化可以发生在各个阶段。
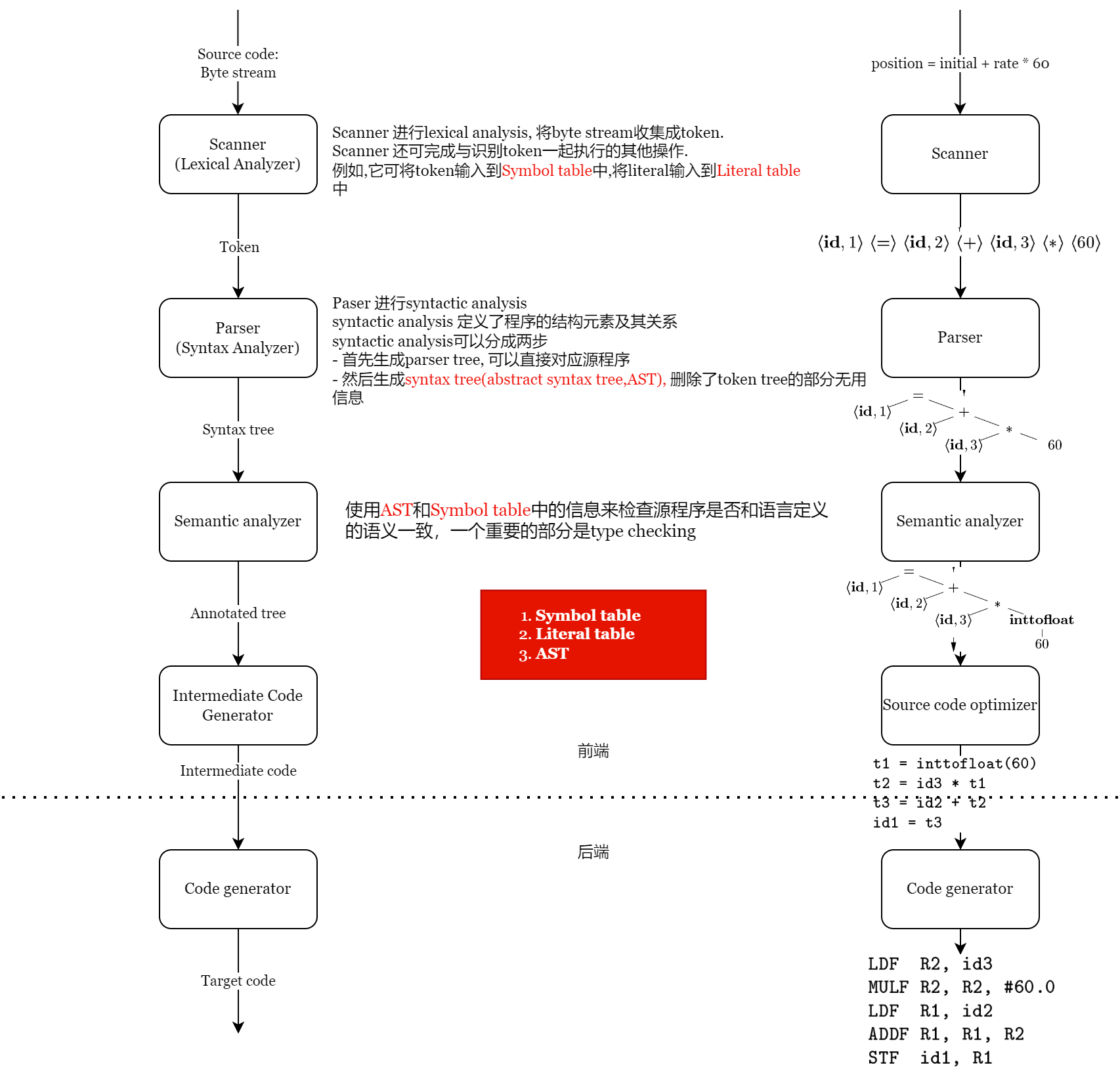
编译过程可以大致分为前端和后端。前端主要是将源代码变成中间代码,后端主要是优化以及生成目标机器码。浙江大学的《编译原理》课程主要讲前端,前端更像一些字符串处理的理论。后端则较少的涉及,后端更接近程序分析。
Lexical Analysis
词法分析(Lexical Analysis) 的主要任务是读入源程序的输入字符,将他们组成 lexemes,生成并输出一个 token 序列(token 和 lexeme 一一对应)。通常,这需要识别 lexemes,过滤注释和空白。
Lexical Analyzer 通常还要和 Symbol table 进行交互,发现标识符时添加到 Symbol table。
有三个概念需要了解。alphabet 是有限符号的集合。string 是符号的有穷序列。language 是给定 alphabet 上任意可数的 string 的集合。
Regular Expression
正则表达式(Regular Expression, Regex)采用归纳定义:
-
归纳基础:
-
空串
ε是一个正则表达式。L(ε) = {ε} -
若
a是∑上的一个符号,那么 a 是一个正则表达式。L(a) = {a} -
归纳步骤:如果 r,s 都是正则表达式,那么
-
(r)|(s)是正则表达式,表示语言L(r) ∪ L(s) (r)(s)是正则表达式,表示语言L(r)L(s)(r)*是正则表达式,表示语言(L(r))*(r)是一个正则表达式,表示语言L(r),这是为了说明括号是没用的。
可以用正则表达式定义的 language 叫做 regular set。为了避免不必要的括号,规定优先级的顺序是 * > 连接 > | 。
正则表达式是存在局限性的,比如他没有计数的功能,他不能匹配类似
n个a b n个a这样的串。
Finite Automata
有穷自动机(Finite Automata)分为两种:
- DFA (Deterministic Finite Automata): 对每一个 状态和输入字符,有且只有一个 下一个状态。
- NFA (Non-Deterministic Finite Automata): 对于相同的当前状态和输入字符,下一个状态不一定是唯一的。
举例:我们通常使用 transition graph 来表示有穷自动机。
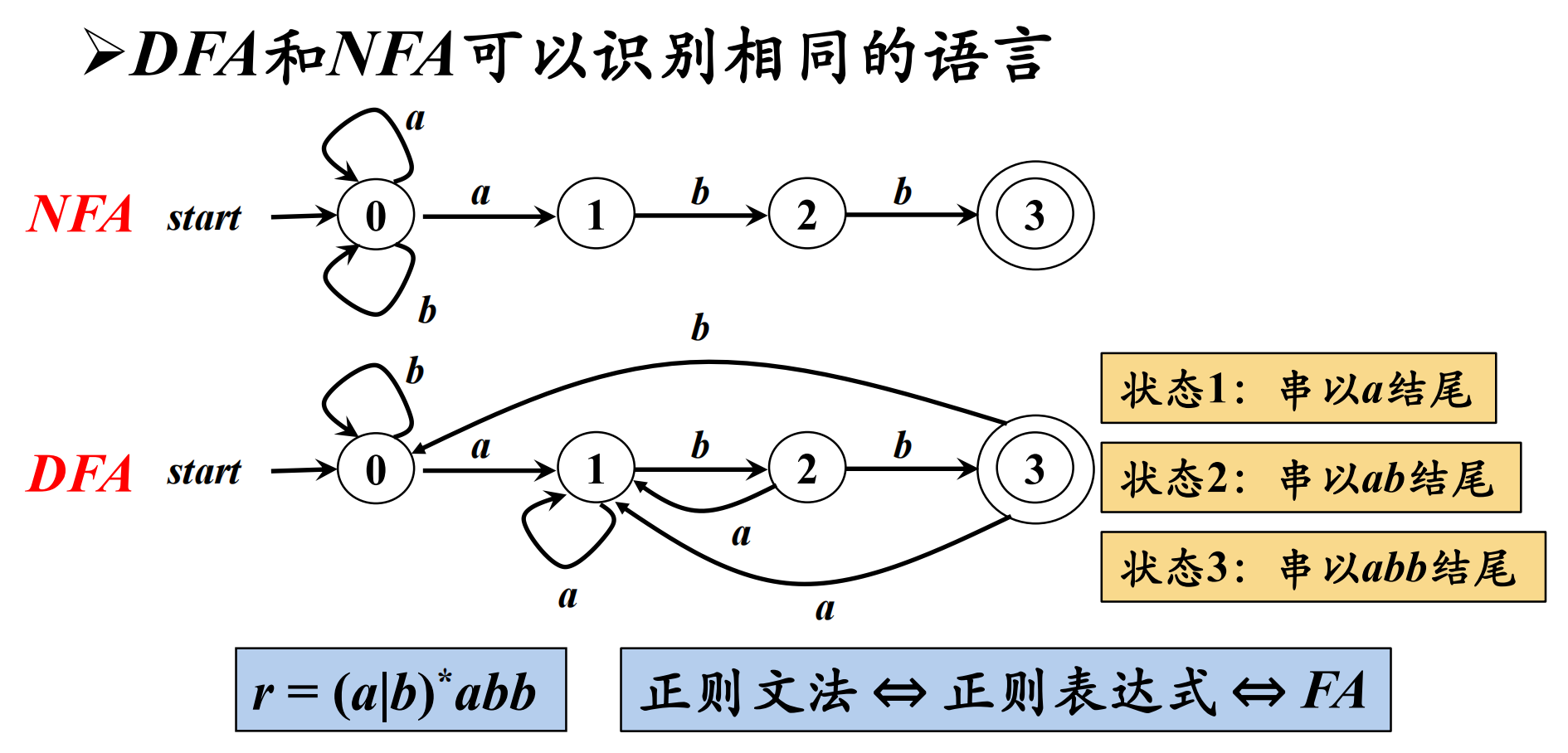
- NFA 和 DFA 具有 等价性。对任何非确定的有穷自动机 N ,存在定义同一 language 的确定的有穷自动机 D,对任何确定的有穷自动机 D ,存在定义同一 language 的非确定的有穷自动机 N。
- 对于任何给定的 DFA,都有一个含有最少量状态的等价的 DFA,而且这个最小状态的 DFA 是唯一的。
Regex -> NFA -> DFA
如果你的直觉足够好,或者有相关的知识储备,你可以看出实际上我们可以用有穷自动机来匹配正则表达式。使用 McNaughton-Yamada-Thompson 算法,我们可以将Regex 转化为 NFA。这个算法的思路是非常简单的,如下图所示:
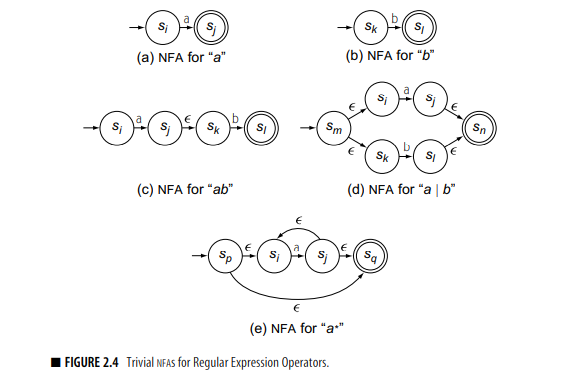
将NFA 转化为 DFA,可以使用子集构造算法。首先了解三个重要的概念(集合),在下面的伪代码会把他们当做函数。
- 状态的
ε-closure(s)。由一个状态 s 出发,可以经过若干个ε转换能到达的状态的 NFA 状态集合。 - 状态集合的
ε-closure(T)。从 集合 T 中的 某一个状态出发,可以经过若干个ε转换能到达的状态的 NFA 状态集合。 move(T, a)。从集合 T 中的某个状态出发,可以通过a转换能够到达的 NFA 状态集合。
然后是构造 DFA 状态转换图。DFA 状态集合,记做 Dstates(也就是图的点),DFA 状态转换关系,记做 Dtran(也就是图的边)。下面是该算法的 Rust 伪代码。
let Dtran = map!();
let Dstates = set!(ε_closure(start),);
let untag = deque!(ε_closure(start),);
while !untag.is_empty() {
let T = untag.pop_front();
for symbol in alphabet {
let U = ε_closure(move(T,symbol));
if Dstate.insert(U) { // DFA增加了一个状态
untag.push_back(U);
}
Dtran.insert( (T,U) ) = a; // 表示 T ---a--> U
}
}
// 因为当前状态 + 输入字符和下一个状态一一对应,所以即使在 NFA 中没有对应的输入(即下一个状态是空集),DFA 中也应该创建一个状态来表示这个空状态。
DFA状态最小化:画出DFA状态转移表后,对于那些在任意相同输入下产生相同输出的状态进行合并。
Syntax Analysis
语法分析(Syntax Analysis) 从 词法分析 获得一个 Token Stream。语法分析器的工作是根据 Token Stream 构造出一个语法分析树,将它传递给编译器的其他部分进一步处理。语法分析器大致分为通用的、自顶向下的和自底向上的,而通用的因为效率太低不被使用,下面会介绍后二者,自顶向下分析 和 自底向上分析。
Context Free Grammar
首先了解 文法 Grammar 的概念。文法是形式语言中字符串的一套产生式规则。这些规则描述了如何用语言的字母表生成符合语法的有效的字符串。文法不描述字符串的含义,也不描述在任何上下文中可以用它们做什么——只描述它们的形式。
Grammar: G=(Vt,Vn,P,S)。意思是说,一个 Grammar 由下面四个元素组成:
- 一个 终结符号 (terminal symbol)集合,有时也叫词法单元 (token)。
- 一个非终结符号 (nonterminal symbol)集合,又是也叫语法变量。每个非终结符号表示一个终结符号串的集合。
- 一个产生式 (production) 集合。
- 指定一个非终结符号位 开始符号 (start symbol)。开始符号表示的是该 Grammar 中最大的语法成分。
例如:stmt -> if (expr) stmt else stmt 这样的规则叫做 production,if 和 () 被称为 terminal symbol,expr 和 stmt 这样的变量表示终结符号的序列,称为 nonterminal symbol。stmt 就是 start symbol。
上下文无关文法 Context Free Grammar 指的是 产生式左侧只能包含一个符号,并且该符号为非终结符号的文法。这个限制是非常重要的。
事实上一共有四种文法,逐级限制。对于α→β:
- 0 型文法:α中至少包含 1 个非终结符
- 1 型文法(CSG 上下文有关) :|α|≤|β|
- 2 型文法(CFG 上下文无关文法) :α ∈ 非终结符
- 3 型文法(RG 正则):A→wB 或 A→w (A→Bw 或 A→w) A/B 代表非终结符
程序设计语言的语法通常是 CFG,通常用 RG 匹配 Token。
还有一些非常重要的概念需要了解:
- 推导(Derivation):简单的说,就是把 production 的右部替换成左部,只替换 1 次就是 directly derive。记做 \(\Rightarrow^0\),若干次替换记做 \(\Rightarrow^*\)。相反的过程就是 归约 Reduction。parsing tree 是推导的图形化表示。
- 语言(Language):由 grammar
G的 start symbolS推导出的所有 sentence 构成的集合称为 grammarG生成的 language,记为L(G)。L(G) = {w /S =>*, w ∈ Vt*}。要证明一个 Language 和 Grammar 对应,需要证明 Grammar 所有能产生的 sentence 都属于 Language,Language 中所有的 string 都能被 Grammar 产生。 - 二义性(Ambiguous): 若 grammar 对同一 sentence 可以产生不止一棵 parsing tree,则称 G 是 ambiguous。要改写二义性文法为非二义性文法
- 划分优先级和结合性
- 引入一个新的非终结符,增加一个子结构并提高一级优先级(优先级的判断)
- 递归非终结符在终结符左边,运算具有左结合性,否则具有右结合性。
回顾一下,Syntax Analyzer 的作用是生成 AST 或 Parsing Tree。其实 parsing tree 是推导的图形化表示。AST 则是精简的 Parsing Tree,一般我们生产 AST。
现在我们手头有一个 Token Stream。那么我们如何进行推导呢去构建 parse tree 呢?主要有两个问题:换哪个 nonterminal symbol? 用哪条 production?。常用的有两种办法:
- 在 Left-most Derivation 最左推导中,总是选择每个句型的最左 nonterminal symbol 进行替换。这个和 top-down parsing 一起使用,也就是从 Parse Tree 的顶向下分析。左句型 (left sentential form)是指推导至该句子的全部左推导。
- 在 Right-most Derivation 最右推导中,总是选择每个句型的最右 nonterminal symbol 进行替换,最右推导也被称为 规范推导。这个和 down-top parsing 一起使用,也就是从 Token Stream 向上构造 Parse Tree。右句型 (right sentential form) 是指推导至该句子的全部右推导。