排列

31. 下一个排列 - 力扣（LeetCode）

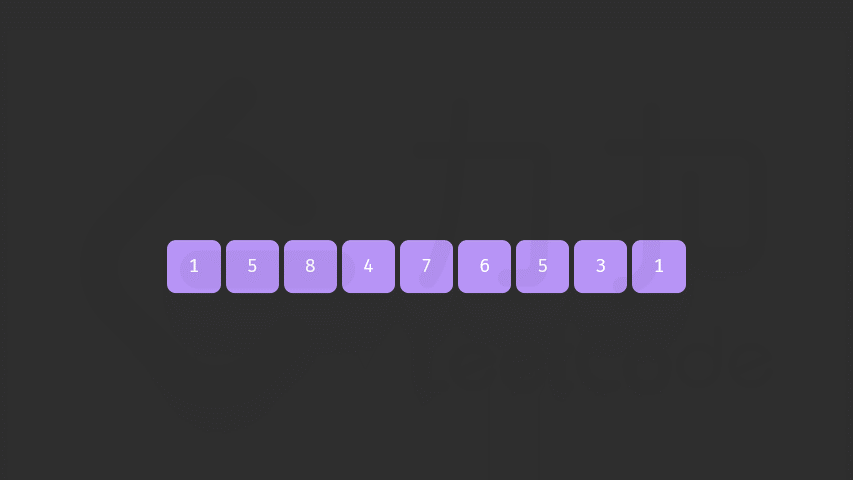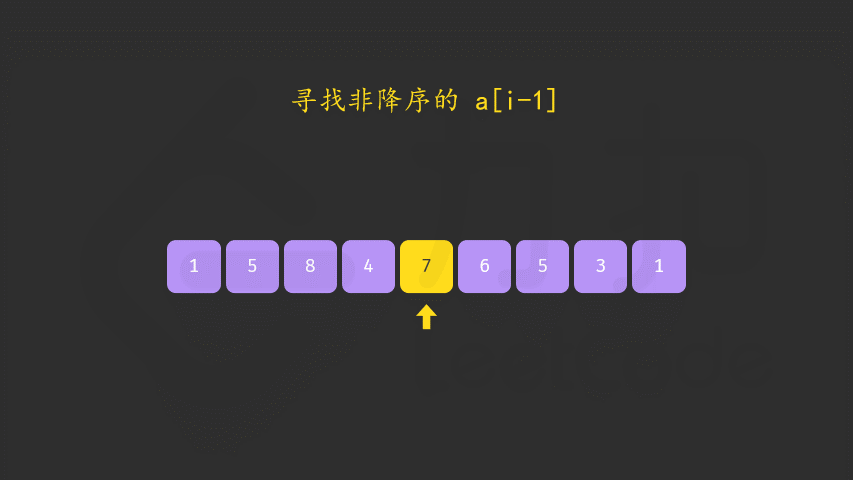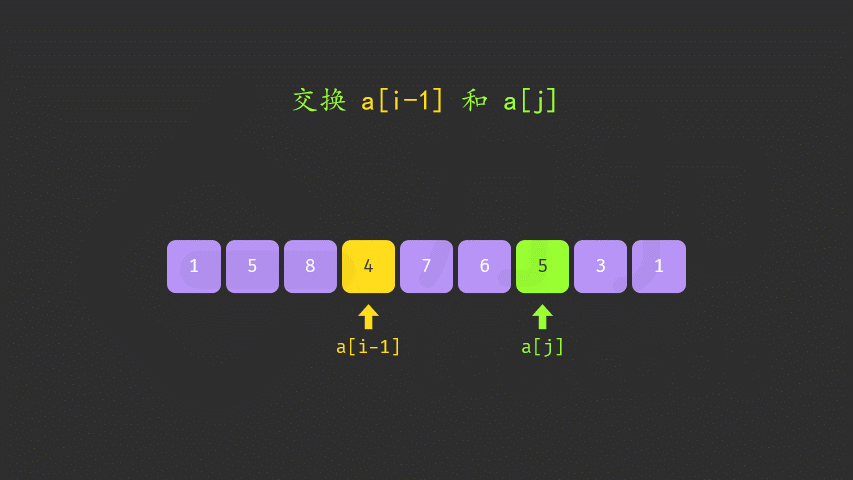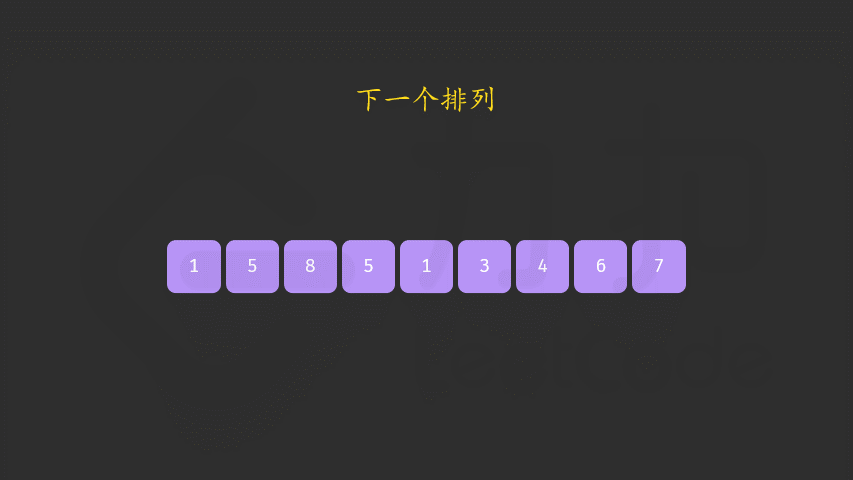
1. 寻找非降序的a[i-1]（倒着找，找不到说明是最后一个排列了）
2. 寻找大于a[i-1]的a[j]（倒着）
3. 交换a[i-1]和a[j]
4. 反转a[i-1]之后的元素

class Solution:
    def nextPermutation(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        i = len(nums) -2
        while i>=0 and nums[i]>=nums[i+1]:
            i -= 1
        if i>=0:
            j = len(nums) - 1
            while j>i and nums[i]>=nums[j]:
                j -= 1
            nums[i], nums[j] = nums[j], nums[i]
        else:  # 对应的情况是最后一个排列，对于这道题应该把else去掉
            return  
        nums[i+1:] = nums[i+1:][::-1]

60. 排列序列 - 力扣（LeetCode） 这道题求的是n个数的第k个排列。考虑到对于n个数，排列情况有\(n!\)种，其中第一个数分别为\(1,2,3\dots,n\)的情况都有\((n-1)!\)种。所以，我们可以求解出第一个数是第\(\lfloor \frac{k}{(n-1)!}\rfloor\)个，然后递归求解其余的数的第\(k \% (n-1)!\)个排列。（从0开始计数）。

class Solution:
    def getPermutation(self, n: int, k: int) -> str:
        fact = [1]
        for i in range(1,n):
            fact.append(fact[-1]*i)
        nums = list(range(1,n+1))

        def dfs(k, n):
            nonlocal nums
            if n == 1:
                return str(nums[0])
            order = k // fact[n-1]
            print(order, nums)
            cur = nums[order]
            nums.pop(order)
            return str(cur) + dfs(k % fact[n-1], n-1)

        return dfs(k-1,n)