跳转至

机器学习

Basic

  • 监督学习（supervised learning）：
    • 分类（classification）：样本属于两个或多个类别，我们希望从已经标记的数据中学习如何预测未标记数据的类别。
    • 回归（regression）: 用于估计因变量（dependent variable, outcome, response...）与一个或多个自变量（independent variable, co-variants, feature...）之间的关系。
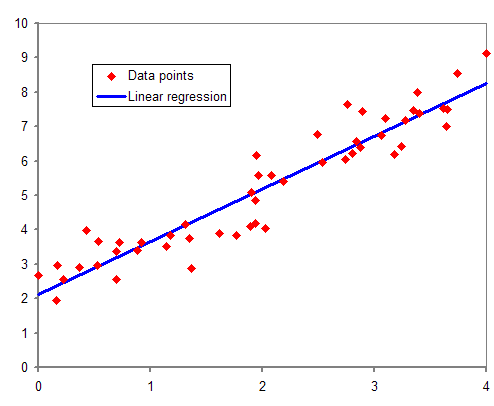
      • 线性回归（linear regression）：这是一个很典型的例子，它认为因变量和自变量之间的关系是线性的(\(y=wx+b\)，更准确的表达是\(y = \vec{w}^T\vec{x} + b\))。线性回归模型可以使用最小二乘法拟合。
      • 逻辑斯谛回归（Logistic regression）：结果只有0和1两种情况，类似于分类问题了。
  • 无监督学习（unsupervised learning）：
    • 聚类（clustering）: 在数据中发现相似示例的组，其中称为聚类。一般我们说无监督学习指的基本上就是聚类。
    • 或者确定输入空间中数据的分布，称为密度估计，或者将数据从高维空间投影到二维或三维以实现可视化。

机器学习在实际操作层面一共分为7步：

  1. 收集数据
  2. 数据准备
  3. 选择一个模型
  4. 训练
  5. 评估
  6. 参数调整
  7. 预测（开始使用）

在理论层面分为3步：

  • 设计一个带未知参数的函数 （即模型）
  • 定义损失函数 L
  • 求解一个优化问题 （让损失函数在数据集上表现的最好）

一些算法

分类算法

Decision Tree: 这也是非常简单经典的Classification算法。

Nearest Neighbor (KNN): 这是非常简单经典的Classification算法。
首先我们需要定义“距离”，常用的有欧氏距离，曼哈顿距离，汉明距离等。注意在实际训练中，将不同特征归一化再算距离。
KNN算法，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，就把该输入实例分类到这个类中。（这就类似于现实生活中少数服从多数的思想）。
那么KNN的参数就只是简单的K了。K太小或者太大都会影响模型的效果。

Bayes Classification Methods

Support Vector Machine: 对于SVM来说，数据点被视为 p 维向量，而我们想知道是否可以用 p-1 维超平面来分开这些点，让超平面和最近的点之间的距离最大化。这就是所谓的线性分类器。
维基百科
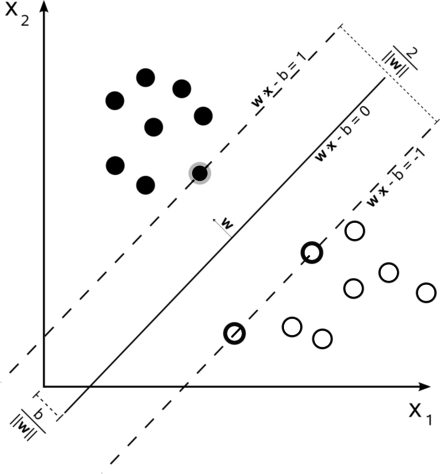
设样本属于两个类，用该样本训练SVM得到的最大间隔超平面。在边缘上的样本点称为支持向量。我们要求的参数就是\(w\)和\(b\)（在二维平面上是数字，p维就是p-1位向量了）。
通过一些修改，可以使用非线形的方法（也就是说不使用平面分开这些点）对数据进行分类；
通过一些修改，可以将数据分成大于2类，最直观的方法是使用\(C^2_n\) 次SVM，然后将\(C^2_n\)个模型全部应用到数据中，最后看分到哪一类的结果最多。

Perceptron

回归算法

在我们开始考虑如何用模型拟合（fit）数据之前，我们需要确定一个拟合程度的度量。 损失函数（loss function） 能够量化目标的 实际值 与 预测值 之间的差距。 通常我们会选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为0。 回归问题中最常用的损失函数是平方误差函数。 当样本\(i\)的预测值为\(\hat{y}_i\)，其相应的真实标签为\(y_i\)时， 平方误差可以定义为以下公式：

$$L(args) = \frac{1}{n}\sum_{i=1}^n \frac{1}{2}(\hat{y}_i-y_i)^2 $$
模型训练的目标就是找到参数\(args\)使得 Loss 最小。对于线性回归来说，我们是可以使用最小二乘法求出参数的解析解的。但是并不是所有的问题都可以求出解析解，这才是机器学习解决回归问题的用武之地。

  • Linear model
    • Linear regression, orthogonal regression
    • Lasso, elastic regression, ridge regression,
    • Logistic Regression (general linear)
  • Non-Linear model
    • MLP, DNN, CNN, RNN, LSTM (Deep learning)
    • Decision Tree, random forest(ML, 2001)
    • Adaboost(JCSS, 1997), Xgboost(KDD, 2016)

CNN(Convolutional Neural Networks, 卷积神经网络)

聚类算法

k-min

一些库

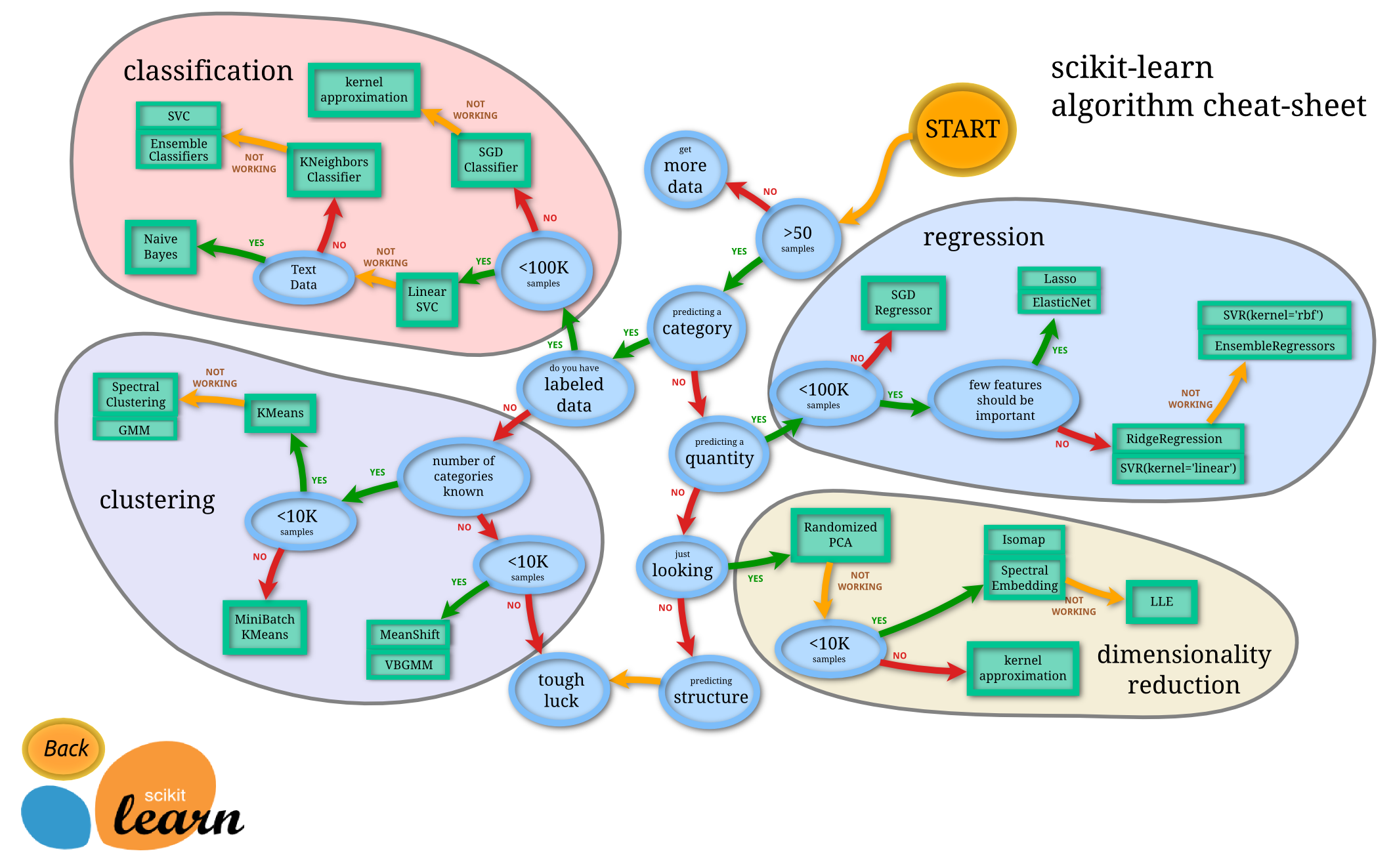
https://scikit-learn.org/stable/